Técnicas Básicas de Contagem
Regra do Produto Se um conjunto A tem |A| possibilidades e B tem |B| possibilidade então existe |A|*|B| formas de combiná-los. Por exemplo, se tenho 4 camisas e 3 calças logo tenho 12 maneiras de distintas de vestir-se. Considere o seguinte exemplo:
Seja a decomposição de um número n em fatores primos p1, …, pk
Cada divisor do número n pode ser escrito como 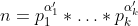 , onde
, onde 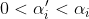 dessa maneira temos
dessa maneira temos  possibilidades para cada fator da multiplicação.Logo, o número de divisores de N dado por d(n) será dado pela seguinte fórmulas
possibilidades para cada fator da multiplicação.Logo, o número de divisores de N dado por d(n) será dado pela seguinte fórmulas
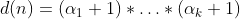
Algoritmo
Algoritmo
#include <stdio.h> #include <stdlib.h> #include <math.h> #define MAX 100 int p[MAX]; int e[MAX]; int cont; void fatora(int n){ int i; int num_divisores; i=2; cont = 0; while(n!=1){ if(n%i==0){ p[cont] = i; while(n%i==0){ e[cont]++; n=n/i; } cont++; } i++; } num_divisores = e[0]+1; printf("n = %d^%d",p[0],e[0]); for(i=1;i<cont;i++){ printf("+%d^%d",p[i],e[i]); num_divisores *= e[i]+1; } printf("\n"); printf("num divisores %d\n",num_divisores); } int main(){ fatora(60); }
SAÍDA
n = 2^2+3^1+5^1
num divisores 12
Lembrando que diminuindo qualquer um dos expoentes da
decomposição de n em fatores primos gera um divisor de n.
Por exemplo,
d = 2^1+3^1+5^0 = 6 é divisor 60
d = 2^2+3^0+5^0 = 4 é divisor 60
Regra da Soma Se um conjunto tem |A| possibilidades e B tem |B| possibilidade então existe |A|+|B| maneiras de A ou B podem ocorrer.
Exemplo: Com quantos zeros termina N!?
Para o número N! ganhar um zero no final, ele precisa ter um fator 10 = 2*5. Para saber o número de zeros no final de N!, precisamos saber o mínimo entre o número de fatores 2 e 5. O número de fatores 5 é menor que o número de fatores 2. Logo, precisamos apenas saber o número de fatores 5.
Seja o número de múltiplos de k menores que n dado por M(k,n).
Logo, o número de zeros no final de N! será dado por
zero(n!) = M(5,n) + M(52,n) + M(53,n)+…+M(5k,n), onde 5k < n
M(5,n) conta o número de múltiplos de 5 menores que n. Só que número 25 tem dois fatores 5. Logo, precisamos contar também o número de múltiplos de 25 menores que n para contabilizar o segundo fator 5 do número 25. E assim, procedemos com todas as potências de 5 possíveis.
Podemos desenvolver esta idéia de outra forma, vamos colocar todos os termos com fator 5 em evidência:
n! = 1.2.3.4.(5.1).6...9.(5.2).11...14.(5.3).16.....(5.m)..(n-1).(n)
Logo, podemos escrever n! da seguinte maneira:
n! = 5(1*2*3*…*m)*L1, onde L1 não contém múltiplos de 5 e m é o número de múltiplos de 5 menores que n. O número de zeros no final de n! é igual a:
zero(n!) = m + zero(m!), onde m número de múltiplos de 5 menores que n
#include <stdio.h> #include <stdlib.h> #include <math.h> int zeros(int n){ int d=5; int num_zeros=0; while(d<=n){ num_zeros += n/d; d *=5; } return num_zeros; } int zeros2(int n){ if(n<5) return 0; else return n/5 + zeros2(n/5); } int main(){ printf("25!=15511210043330985984000000\n"); printf("numero de zeros: %d\n",zeros(25)); printf("numero de zeros: %d\n",zeros2(25)); }
OUTPUT
25!=15511210043330985984000000
numero de zeros: 6
numero de zeros: 6
Um comentário:
Boa Wladmir, pena que eu não conheci a olimpíada na minha época de aluno de graduação.
David Sena
Postar um comentário