A indução matemática é uma técnica extremamente importante para demonstrar que uma propriedade é válida para todos os números naturais (ou a partir de um certo valor). Os números naturais pode ser definido como o menor conjunto definido pelas seguintes regras:
Observe que os inteiros também satisfazem essas duas regras.
Quando fazemos uma prova por indução, mostramos que uma certa propriedade também é capaz de satisfazer essas duas regras simples. Com isso, obtemos que a propriedade em questão é válida para todos os números naturais. Primeiramente, temos que mostrar que a propriedade é verdadeira para um caso inicial chamado de caso base. O próximo passo é mostrar que toda vez que P(n-1) é verdadeira, P(n) também é verdadeira para n>0. Esse último passo é chamado de passo indutivo. A hipótese que P(n-1) é verdadeira é chamada de hipótese de indução. Ao encerrar estes dois passos, concluímos que P(n) é verdadeira para todos os números naturais.
Uma boa analogia para o processo de indução é o efeito dominó. Imagine uma coleção de dominós colocados numa sequência (formação) de tal forma que a queda do primeiro dominó (caso base) força a queda do segundo (passo de indução), que força a queda do terceiro (passo de indução), e assim sucessivamente, até todos os dominós caírem.
Exemplo:
Mostre que P(n) é valida para n >= 8
P(n) = é possível obter qualquer valor n centavos ou mais usando apenas moedas de 3 ou 5 centavos
caso base
P(8) é verdadeira
8 = 3+5
Hipótese de Indução
Suponha que a propriedade P é válida para um certo n-1 >=8, ou seja, é possível obter n-1 da seguinte maneira:
n-1 = 3a + 5b a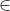 N e b
N e b 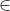 N
N
( Observe que não sabemos qual é o valor de n-1.)
Passo de Indução
Vamos mostrar que a propriedade é válida para n, ou seja, temos que mostrar que é possível obter o valor n sabendo "a resposta" para n-1.
Observe o seguinte:
Saída
Entre com um valor maior que 8:8
8=3*1 + 5*1
Entre com um valor maior que 8:9
9=3*3 + 5*0
Entre com um valor maior que 8:10
10=3*0 + 5*2
Entre com um valor maior que 8:11
11=3*2 + 5*1
Entre com um valor maior que 8:12
12=3*4 + 5*0
Entre com um valor maior que 8:13
13=3*1 + 5*2
Entre com um valor maior que 8:14
14=3*3 + 5*1
Entre com um valor maior que 8:15
15=3*5 + 5*0
Entre com um valor maior que 8:16
16=3*2 + 5*2
Entre com um valor maior que 8:17
17=3*4 + 5*1
Entre com um valor maior que 8:18
18=3*6 + 5*0
Agora, chegou a sua vez!!!
Mostre que P(n) é valida para n >= 12
P(n) = é possível obter qualquer valor de postagem de n centavos ou mais usando moedas de 4 ou 5 centavos.
Leia também:
Uma boa analogia para o processo de indução é o efeito dominó. Imagine uma coleção de dominós colocados numa sequência (formação) de tal forma que a queda do primeiro dominó (caso base) força a queda do segundo (passo de indução), que força a queda do terceiro (passo de indução), e assim sucessivamente, até todos os dominós caírem.
Exemplo:
Mostre que P(n) é valida para n >= 8
P(n) = é possível obter qualquer valor n centavos ou mais usando apenas moedas de 3 ou 5 centavos
caso base
P(8) é verdadeira
8 = 3+5
Hipótese de Indução
Suponha que a propriedade P é válida para um certo n-1 >=8, ou seja, é possível obter n-1 da seguinte maneira:
n-1 = 3a + 5b a
( Observe que não sabemos qual é o valor de n-1.)
Passo de Indução
Vamos mostrar que a propriedade é válida para n, ou seja, temos que mostrar que é possível obter o valor n sabendo "a resposta" para n-1.
Observe o seguinte:
- Se trocarmos uma moeda de 5 por duas moedas 3 podemos partir de um valor n-1 para um valor n.
- Se trocarmos 3 moedas de 3 por 2 moedas de 5 podemos partir de um valor n-1 para um valor n.
Observe que precisamos ter pelo menos 1 moeda de 5 ou 3 moedas de 3 para realizar essas transformações. A partir do valor 8, uma dessas duas condições sempre acontece. (Tenha certeza disso!).
Por hipótese de indução, temos que P(n-1) é válido, ou seja,
n-1 = 3a + 5b a 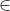 N e b
N e b 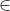 N
N
Se b >= 1 então
a’ = a+2
b’ = b-1
n+1 = 3a’ + 5b’
Senão
//O valor de b=0,a >= 3 e n-1>=9
a’ = a-3
b’ = b+2
n+1 = 3a’ + 5b’
Código
#include <stdio.h> int main(){ int n; while(1){ printf("Entre com um valor maior que 8:"); scanf("%d",&n); if(n<8) break; int i; int a[n+1]; //quantidade de 3's int b[n+1]; //quantidade de 5's a[8] = 1; b[8] = 1; for(i=9;i<=n;i++){ if(b[i-1]>=1){ a[i] = a[i-1]+2; b[i] = b[i-1]-1; }else{ a[i] = a[i-1]-3; b[i] = b[i-1]+2; } } printf("%d=3*%d + 5*%d\n",n,a[n],b[n]); } return 0; }
Saída
Entre com um valor maior que 8:8
8=3*1 + 5*1
Entre com um valor maior que 8:9
9=3*3 + 5*0
Entre com um valor maior que 8:10
10=3*0 + 5*2
Entre com um valor maior que 8:11
11=3*2 + 5*1
Entre com um valor maior que 8:12
12=3*4 + 5*0
Entre com um valor maior que 8:13
13=3*1 + 5*2
Entre com um valor maior que 8:14
14=3*3 + 5*1
Entre com um valor maior que 8:15
15=3*5 + 5*0
Entre com um valor maior que 8:16
16=3*2 + 5*2
Entre com um valor maior que 8:17
17=3*4 + 5*1
Entre com um valor maior que 8:18
18=3*6 + 5*0
Agora, chegou a sua vez!!!
Mostre que P(n) é valida para n >= 12
P(n) = é possível obter qualquer valor de postagem de n centavos ou mais usando moedas de 4 ou 5 centavos.
Leia também:

2 comentários:
Se a pressão psicológica + trabalhos semanais + provas semanais funciona para o aluno 1, se funciona para o aluno j, e se funciona para o aluno j+1, então todos os alunos vão estudar para prova.
Entendi direito? :)
David Sena
Falta mostra que existe uma maneira de transferir de aluno j para o aluno j+1 :)
Postar um comentário