O resultado mais importante sobre os números primos é o chamado Teorema Fundamental da Aritmética que garante que todo número maior que 1 pode ser decomposto em fatores primos. Vamos apresentar o algoritmo que executa mais operações, mas que é mais fácil de ser entendido. O algoritmo consiste em testar os números menores ou iguais 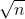 e ir dividindo a medida do possível:
e ir dividindo a medida do possível:
#include <stdio.h> #include <math.h> #include <vector> #include <iostream> #include <stdlib.h> using namespace std; vector <int> fatora(int n){ int i,limite; vector <int> primos; i=2; limite = (int)sqrt(n); while(n > 1 && i<=limite){ //se i divide n entao i eh primo retira todos os fatores i de n while(n%i==0){ primos.push_back(i); n=n/i; } i=i+1; } //se i >= raiz de n entao n eh primo if(n>1) primos.push_back(n); return primos; } int main(){ vector <int> primos; primos = fatora(120); printf("%d",primos[0]); for(int i=0;i<primos.size();i++) printf("*%d",primos[i]); printf("\n"); system("PAUSE"); }
SAÍDA
2*2*2*2*3*5
Pressione qualquer tecla para continuar. . .
Podemos provar que nenhum número composto será adicionado no vetor primos.
Teorema: O algoritmo fatora encontra a decomposição em fatores primos.
Prova: Suponha por absurdo que um número não-primo foi adicionado no vetor primos (vetor que guarda a decomposição em fatores primos). Seja d o menor número não-primo adicionado no vetor primos. Pelo Teorema Fundamental da Aritmética, d também pode ser decomposto em fatores primos. Considere a seguinte decomposição de d = p1*p2*...*pk onde pi < d. Logo, existe um primo pi que foi “pulado” durante o algoritmo uma vez que pi < d. Absurdo, todos os números menores que d são testados antes de d.
O pior caso desse algoritmo tem a seguinte complexidade:
Programa em JavaScript que descobre a decomposição em fatores primos utilizando esse algoritmo
O pior caso desse algoritmo tem a seguinte complexidade:
A segurança do sistema RSA depende da dificuldade da fatoração de um número n em fatores primos. Vamos imaginar que queiramos quebrar a criptografia de um sistema RSA com uma chave de 1024 bits. Logo, n ~ 21024 ~ 21000~ (210)100 ~ (103)100~ 10300. Precisamos testar aproximadamente 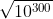 ~10150 números. Considerando que seja possível testar 109 fatores por segundo. Para testar todos os valores possíveis ~10141 segundos ~ 10130 milênios.
~10150 números. Considerando que seja possível testar 109 fatores por segundo. Para testar todos os valores possíveis ~10141 segundos ~ 10130 milênios.
Programa em JavaScript que descobre a decomposição em fatores primos utilizando esse algoritmo

3 comentários:
Quando eu inventar o computador quântico fatorar primos vai virar problema do passado :)
David Sena
Já ouvi falar que mesmo com os computadores quânticos o problema se mantém.
Fabio Dias
eu descobri um algoritmo capaz de descriptografar o sistema rsa em um tempo aceitável.... na verdade se esse algoritmo fosse utilizado numa chave pública de mais de 2.000 dígitos o algoritmo encontra o número primo em no máximo 3 meses, parece muito mas os melhores computadores do mundo hoje, levariam milhares de ano....
Postar um comentário