Teste de Primalidade

Na escola, aprendemos que os números primos são especiais: ele tem exatamente dois divisores 1 e n e todo número maior que 1 pode ser representado de maneira única por produto de números primos (chamado de fatores primos). Este resultado é conhecido como Teorema Fundamental da Aritmética. 

Na Grécia Antiga, Euclides já tinha percebido que os primos eram os blocos fundamentais, os átomos, que constituem o edifício dos números inteiros. Vários matemáticos tentaram encontrar uma fórmula para descobrir os primos, mas, até agora, nenhum matemático conseguiu a solução desse antigo quebra-cabeça. 

Euclides (300 AC) formulou e respondeu a seguinte pergunta sobre os primos:

Os números primos são finitos ou infinitos?

Para responder esta pergunta, ele utilizou um método de prova chamada redução ao absurdo.

Prova: Suponha por absurdo que a quantidade de números primos é finita e pode ser listada da seguinte maneira P = {p1,...,pk}. Seja N definido como o produto de todos os primos somando mais 1:

N = p1*...*pk + 1

Nenhum primo pode ser divisor de N, pois para todo pi, N % pi = 1. Como nenhum primo é divisor de N então N não pode ser dividido por nenhum primo. Portanto, N é também um número primo,  mas  N não pertence ao conjunto P. Absurdo!

Até onde eu preciso testar para saber se um número é primo ou não?

Se n não é primo, então o menor divisor de n, d_0, menor ou igual a .

Este resultado também pode provar utilizando a redução por absurdo.

Prova: Suponha por absurdo que n não é primo e o menor divisor de n d₀ maior que  .

d₀ > 

d₀² > n

d₀ > n/d₀

Temos que d₀ é um divisor (e fator primo) de n e podemos escrever n = d₀*k onde k 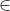 Z. Temos também n/d₀ é um divisor de n, uma vez que, podemos escrever n = (n/d₀)*d₀  e d₀  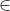Z.

Absurdo, d₀ é o menor divisor de n e existe um outro divisor de n, n/d_0, menor que d_0.

#include <stdio.h>
#include <math.h>
#include <stdlib.h>

/*
funcao ehprimo(n) retorna 0, se n nao eh primo 
                          1, se n eh primo

se i eh divisor de n entao n nao eh primo

se nenhum numero 2<=i<=sqrt(n) eh divisor de n entao n eh primo 
*/
int ehprimo(int n){
  int limite;
  limite = (int)sqrt(n);
  for(int i=2;i<=limite;i++){
    if(n%i==0) return 0;
  }
  return 1;
}

int main(){
  int cont=0;  
  for(int i=2;i<=1000000;i++){
    if(ehprimo(i)) { 
      cont++;
    }

  }
  printf("numeros primos menores que 1000000: %d\n",cont);
  system("PAUSE");

}

Saída
numeros primos menores que 1000000: 78498
Pressione qualquer tecla para continuar. . .

Podemos conferir o resultado aqui:
http://www.wolframalpha.com/input/?i=number+of+prime+from+1+to+1000000


Gauss tentou responder uma pergunta interessante sobre os números primos:
Quantos primos existem até um certo número n?
Gauss era fascinado por um suplemento do seu livro de logaritmos que trazia uma tabela de números primos. Os logaritmos eram previsíveis mas os primos eram completamente aleatórios. Parecia não existir qualquer conexão entre os logaritmos e os primos. Gauss denotou a quantidade de números primos até x e observou essa estranha relação entre e log(x).



A fórmula que ele encontrou é uma boa aproximação para a quantidade de  números de primos até um certo número.

Confira aqui:
Comparação até 100
Comparação até 1000
Comparação até 10000
Comparação até 100000
Comparação até 1000000

Links relacionados:
http://elementosdeteixeira.blogspot.com/2012/02/o-desafio-dos-numeros-primos.html